モーダルインターチェンジはノンダイアトニックコードを「誘導」しない
7割がた自分の備忘録として。
コード理論の中に「借用和音」とか「モーダルインターチェンジ」という用語がある。
ネット上にもごろごろ転がっていて、ググればそれに関する記事はいくらでも出てくる。
ギターのためのコード理論体系 | 清水 響 |本 | 通販 | Amazon から引っ張ってくると、
異なるモードやスケールからダイアトニックコードを借りてくる手法をモーダルインターチェンジ(Modal Interchange)、借りてきたコードをモーダルインターチェンジコードと呼びます。
英書ですが、"Jazzology" https://amzn.to/3rCW9es からも引っ張ってくると、
Modal interchange (sometimes referred to as borrowed harmonies, mode mixture, or just mixture) is the use of a chord from a parallel (having the same root) mode or scale.
と、まあどこも大体同じようなことを書いています。
これは説明通り、「モードやスケールをたくさん知っておくと、そこから柔軟にコードを持ってきて使っていいよ」という話である。が、いくつか注記をしたい。
「コードを持ってくる」という言葉には以下の2つの意味合いがある:
- ルートがダイアトニックであるコードを持ってくる。つまり、コードクオリティのチェンジを行なう。
- ダイアトニックでないルートのコードを持ってくる。つまり、本当にコードを借りてくる。
おかゆの今の理解としては、
ように思っております。
"jazzology" にあるように、Modal interchangeは、mode mixtureとか、もっと単純に mixture とも呼ばれるもので、そのコードの「モードを交換したり、混ぜたりする」手法と理解すると、 2.の方法はモーダルインターチェンジの範囲を逸脱しているように思います。そこは頑張って two-fiveとか、きちんとした力学エンジンを論拠にしてほしい。
というわけで、おかゆとしては、モーダルインターチェンジは「そのコードがもつモードを交換すること」…ざっくりいうと、「コードクオリティをチェンジすること」とほぼ同義だと理解する。
にもかかわらず、クオリティチェンジをしたいならモーダルインターチェンジの概念はいらん、とさっき言いましたが、これは正確にいうと、
「クオリティチェンジの着想を得る材料として、モーダルインターチェンジは不要」
ということです。クオリティチェンジに関する定理はただひとつで、「クオリティチェンジは勝手に好きにすればよい」なんじゃないか?というわけです。
なぜ?
我々が基本的に使うスケールは、以下のものが95%です:
- メジャースケール
- メロディックマイナー
- ハーモニックマイナー
- ハーモニックメジャー
- ホールトーンスケール
モーダルインターチェンジの教えによれば、我々はクオリティチェンジを、この4つのスケールに基づいて好きにしてよいということになる。
……ところで、我々はそもそもどんなクオリティを知っているかというと、
- Δ
- m7
- mΔ
- 7
- φ7; m7(b5)
- o7; dim7
- augΔ
- aug7
の8種と、あとはsus系くらい。
令和の時代、音楽理論の本をめくれば、モーダルインターチェンジの前に、はるか前に、コードクオリティの話が記載されており、 モーダルインターチェンジに着想を受けなくても、教育課程的に、そこから着想可能なコードクオリティはとっくに学習済なわけです。
というわけで、クオリティチェンジに、わざわざモーダルインターチェンジのアイデアはいらん、ということになる。
補足:たまごとにわとりの話
では、令和の時代の学習者が初期に学ぶであろうコードクオリティはどこからやってきたのか?という話はもちろんあって、
詳しい歴史は知らないが、「各スケールから導き出されるコードに現れるクオリティを片っ端から記号化していった」のかもしれず、
そのおかげで、私たち令和の人間は、その整理された記号を初期に学習できているかもしれない。
そう考えると、モーダルインターチェンジの概念はクオリティチェンジの基盤を築いているといえる。
とはいえ、時代にそぐわない。
本当にモーダルインターチェンジはいらんのか? その1
結論をいうと、必要ではある。ただしそれは、ある1つのコードのクオリティチェンジの現象のためではなく、隣接するコードとの関係性を整えるために。
クオリティチェンジはもちろんその性質上、その際にいくつかのノンダイアトニックノート(nDN)を導入することになるが、みだりにチェンジするとnDNが大量に発生して調性が死ぬ。
じゃあどうすればいいかといえば、短い範囲内での(あるいは1曲通しての)クオリティチェンジは同じnDNをリユースしあうような制限を設けるアイデアが浮かぶ。
このときに発生するロジックをうまく理解するために、モーダルインターチェンジはツールとして有用となる。同じモードを使いまわしてチェンジすれば解決するからですね。
本当にモーダルインターチェンジはいらんのか? その2
もうひとつは、これもクオリティチェンジそのものとは関係がなく、チェンジしたあとの話である。「チェンジしたコードの上で何を鳴らせばいいのか?」をどう対処すればいいか?
つまりテンションの話であるが、大量のケーススタディが発生するこの状況では「名前空間」が必要となる。そのリソースは間違いなくモードにあり、モーダルインターチェンジの概念が活躍する。
そのチェンジしたコードをどんなテンション(気分)で弾くのかを、テンションノートを含んだ命名によって記述しつくす必要がある。間違いなく潤沢にあるモードの名前空間が役に立ちますね。
おわり
おわりです。
つづきます
もう少し続けることにする。
そういえば、「借用和音」という用語は、モードから借りてくる以前に、他の調から借りてくるという意味合いもあったのだった。
ただし、トーナルセンターの異なる別の調からコードを借りてくると見るよりも、同じトーナルセンターの異なるモードから借りてくると見たほうが見通しがよい(思考コストが低い)。
その意味でモーダルインターチェンジという概念はやっぱり価値はある。
SoundQuestから
インターネットで最も信頼できる(とおかゆの考えている)SoundQuestでも同様にモーダルインターチェンジの章があります。
前述の「パラレルマイナー」を拡張させよう、という流れ。その中の終盤、『「解釈」とはなにか』の節から引用:
ただしこの“解釈請負人”に何でもかんでも任せる方法は、ちょっと「ニワトリとタマゴ」というか、怪しいところもあります。すなわち、「フリジアンにモード交換してるから、レミラシにシャープがつくんだよ」といういかにもそれらしい説明ですが、これは「レミラシにシャープがついてるから、フリジアンへのモード交換ってことにしたよ」という、完全な“後出しジャンケン”でもあります。ましてや「対応スケールがないなら新しく名前をつければいいじゃない」というスタンスなので、理屈上は(主音を含むコードなら)あらゆるコードを「○○スケールからの借用です」で解釈できることになります。
しかしこのやり方では、なぜこのタイミングでフリジアンにスッと交換ができるのか、なぜ進行先がもっぱらIΔに限られるのかといった、「一歩先の“なぜ”」には答えられません。 こうした技法を自分の音楽性を高めるために身につけるならば、対応するスケールを見つけて終わりではなく、展開の中でそのコードが持っている音楽的意味をきちんと考えるべきです。この♭IIΔの場合、やはり♭II7との類似性は無視できない分析要素になるはずです。
個人的にはこの理解がいちばん誠実感があって好き。「テンションも含めて借りてくる」ので、そういう名前をつける。けど、やっぱり題の通り「誘導」はされない。
また、SoundQuestでは、モードと関連するクオリティチェンジについては、別章(CSTの範囲)にて、『キー非依存のモード交換』という節で論じられている:
いちおう広義の「モーダル・インターチェンジ」の一種と言えそうですが、しかし微妙にやっている内容が異なるので、同じ言葉をあててしまうと逆に紛らわしそうです。ここでは便宜的に、モードを交換するということで、単に「モード交換Mode Change/モード・チェンジ」と呼ぶことにします。
ここでは、モーダルインターチェンジとは微妙にちがうから、「モードチェンジ」と呼ぶことにしていますね。
この立て付けはかなり良くて、「調を入れ替える」のをモードに拡張したのが「モーダルインターチェンジ」、クオリティチェンジをモード(テンション情報)にまで拡張したのが「モードチェンジ」。確かに!という感じ。
この2つは実質的には似たような操作になるが、根底にもつスタンスがちがうように思える。テンデンシー(傾性)重視か、サウンド重視か。
とはいえ、いずれにせよ、クオリティチェンジの力学にはうまく答えられないように感じる。
実践に向けての試論
さて、どうやってクオリティチェンジをしようか?という話になる。
"The jazz theory book" では度々「可能な限りコードではなくキーを考えることを学べ」と出てくる。
CSTはむしろキーに囚われないための理論だったので、このフレーズは非常に不思議だが、しかし実際有意義に思う。
(……というより、正しく表現すると、CSTとは表記のキー非依存性を目指しているのかもしれない。アドリブと意思疎通のために。)
クオリティチェンジの仮説(恐らくどこでも書かれている)は3+1つ:
- 元のコードクオリティの1音を変化させることができる。
- 近辺で生じたモーダルインターチェンジに便乗できる。
- 別の力学特性によってクオリティを変化させる。
- 元のコードクオリティのルート省略形として導入できる。
4についてはクオリティチェンジの域を超えてコード置換の領域に入ってしまっているが、項目として挙げておく。
1について
繰り返しになるが、我々の慣れ親しんだ5つのスケールに登場するコードクオリティは以下の8種である:
- Δ
- m7
- mΔ
- 7
- φ7; m7(b5)
- o7; dim7
- augΔ; +Δ
- aug7; +7
(susについては除いている。というのも、susはそのチェンジによってモードを変えなくてよく(要検証)、その意味で「オプショナルな変位」であるからだ。)
これらの「1音変化」の関係をグラフで書くと次のようになる:

ただし、対称性を込めて上記に6およびm6を加えた。トライアドも一応書いておく:
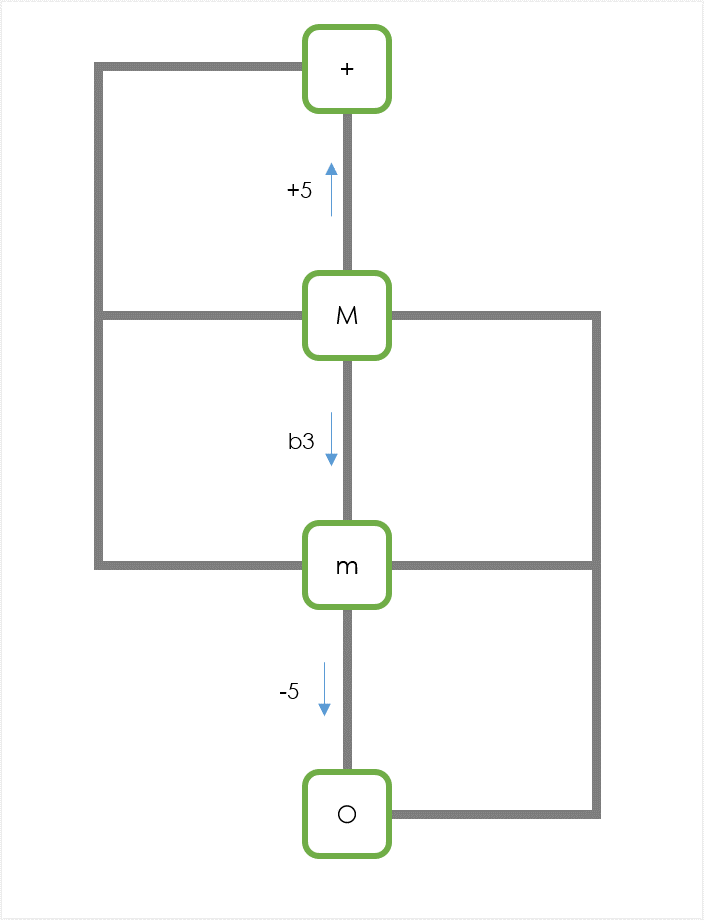
1.の規則「元のコードクオリティの1音を変化させることができる」に従えば、上記グラフの隣接ノードにクオリティチェンジできるということになる。
2
1や3の規則によって生じたnDNを包含するモードを想定し、そのモードとのインターチェンジを考えることで、近辺のコードのクオリティチェンジに使うこともできる。
(ここにいずれ事例が入る)
3
これはもっぱらセカンダリードミナントやtwo-fiveによる。セカンダリードミナント力学によってコードをセブンスにチェンジできる。
4
これは特にルートにnDNが来るときに考えられる。
ベイズの公式の「事後確率」について
はじめに
最近、ベイズ的なアレを色々調べているのだけど、結構面白い。
ただ、少し気になることがあり、かつ、それがあまりウェブに記載がなかったので、メモがてら書いておくことにした。
統計モデリングと「ベイズの公式」
フラットな立場でいえば「統計モデリング」や「確率モデリング」、少し匂いをつけると「ベイズモデリング」は、データ解析者がなんかしらのパラメータを内部にもつ確率モデルを設定し、そのパラメータを観測されたデータに基づいて適宜更新していく一連のプロセスによって成り立つ。
それで、どのようにして確率モデルを更新していくか?というと、「ベイズモデリング」の名の通り、かの有名な「ベイズの公式」を用いる。よく言われるのは「原因」と「結果」の関係だが、もう少しフラットに説明する。
ある対象がどんな状態なのかを、その対象が呈する表現から推測する。対象への理解として、一般的な知識や経験に基づいて、どれくらいの確率で各状態になるのかが分かっている($P(State)$が既知)。さらに、その対象が或る状態だったときに、注目している表現を呈する確率も知っている($P(Expression | State)$が既知)。このとき、ある表現が観測されたときの、各状態でありうる確率を求める。
今回の文脈では、対象とは解析者が措定した確率モデルのことにほかならず、「状態」として、確率モデルのパラメータを $\theta$, 「表現」として、観測されうるデータを $Data$ とすれば:
$$ P(\theta | Data) = \frac{P(Data | \theta)P(\theta)}{P(Data)} = \frac{P(Data | \theta)P(\theta)}{\sum_{i} P(Data|\theta_i)P(\theta_i)} $$
がベイズの公式となる。この式は、繰り返しになるが、「今の確率モデル($\theta$をパラメータとするモデル)のもとで、仮に $Data$ が観測されたときに、確率モデルのパラメータ として $\theta$ が、より正確である(現実に即している)確率」を表している。
この時点では、$Data$ はまだ「実際に観測されたデータ」ではなく「観測されうるデータ」として、つまり、「もしも話」だということに留意しておく。
世の中的には広く、これの左辺($P(\theta | Data)$)を事後分布と呼び、一方で右辺の $P(\theta)$ のことを事前分布と読んでいる。
おかゆは、この状態で「事後確率」と呼ぼうとするのはちょっと早漏なんちゃうかな?と思っている、というのがこの記事のメイン。
「モデルの更新」をきちんと書く
「事前確率 → 事後確率」という「更新」のプロセスが、ベイズの公式に含まれているかと言われると甚だ怪しい。上述したように、ベイズの公式が述べるのは「もしも話」であって、「実際に云々のデータが観測され、更新した後の $\theta$ の確率」それ自体を語っているわけではない。非常に雑にいうと、モデルをどう更新するのかは完全に人為的な営みであり、ベイズの公式が提示してくる $P(\theta | Data)$ は更新方針のいち材料でしかない。……という立場を取ると、$P(\theta | Data)$ のことを「事後確率」と呼ぶのは、ベイズの公式の時点では早計だというように思うわけです。
モデルの更新は、ベイズの公式ではなく、人の手によって行われるというのが、まず1つ目のメモです。
つまるところ、$P^{\rm{new}}(\theta)$ をどうやって決定しようかという話です。これはある種、アルゴリズム的な話でもありますが、確率論的な裏付けがほしいです。というわけで:
$$ P^{\rm{new}}(\theta) = \sum_{i} P(\theta | data_i) P(data_i) $$
によって更新することにします。「云々のデータがこれくらいの確率で出る」という情報と、ちょうど先ほどベイズの公式で求めた「云々のデータが出たときの、パラメータ $\theta$ の当たり具合」という情報を用いれば、なるほど、モデルは更新できそうです。
さて、データの観測を一発勝負にします。一度だけ観測し、あるデータ $data_k$ が得られた場合、その確率分布は:
$$ P(Data = data_i) = \Delta_{i, k} $$
とできるはずです。ここで、今は簡単のために離散分布を考えているので、$\Delta_{i, k}$はクロネッカーのデルタです。連続分布を考えるなら、ディラックのデルタにしてください。
今まさにそのサンプリングによって得られるデータの確率は、実際の観測によって収束した、という風に考えたわけです。
得られるデータの確率分布(というか、$data_k$ が得られたという事実)、および、ベイズの公式の左辺項を用いて、結果的に更新後の確率モデルパラメータの分布は:
$$
P^{\rm{new}}(\theta) = \sum{i} P(\theta | data_i)P(data_i) = \sum{i} P(\theta | data_i) \Delta_{i, k} = P(\theta | data_k)
$$
となり、結果的に、$P(\theta | data_k)$ が確かに「事後確率」として採用できることが示せました。
まとめ
モデルの更新は、ベイズの公式ではなく、人の手によって行われるものであるはずです。そこで、いわゆる「ベイズ更新」を用いる際のその手の動かし方をきちんと書くことで、確かにふつう「事後確率」と呼ばれるものが、更新後の分布として採用されることを示しました。
このプロセスを経ると、確かにベイズの公式の左辺項は「事後確率」と呼んでいいですが、ベイズの公式を「事後確率を算出するための式」として権威づけるのは、ちょっとやりすぎな感じはしますよね。
おまけ
Newton誌は毎月買っています。
— 黒木玄 Gen Kuroki (@genkuroki) July 29, 2020
Newton 2020年9月号は、「主観確率」「ベイズ主義」でベイズ統計について説明する有害解説のA級戦犯の一人である松原望さんが監修しているベイズ統計特集。
期待通りに「ベイズ主義」「主観確率」のひどい解説が炸裂しているページがありました。 #統計 https://t.co/8yTU53iWsM
やっぱベイズ更新って「もし云々のデータが出た場合、今のモデルでパラメータがθkの可能性って低い/高いね」があって、かつ、「そして実際にそのデータが出た」という観測によるデータ確率の収束があるから、「変更」の道がひらけるよなあ
— おかゆさん (@oka_iu_tcan) September 21, 2020
人工言語って虚無じゃないですか(お気持ち創作論)
にわかに流行っているので、おかゆも書きたくなりました。
【参考】
一本の筋に載せて長文かける気がしないので、小さなコラム単位で色々書いていこう、と思って1編書いたんですが、なんか微妙だったんでやっぱり一本の筋で載せれるところだけ書きます。
の前に:誰?
おかゆって何してたんかなっていうのを書いておいたほうがいい気がしたので書きます。
いちばん最初の発端はエスペラントで、本格的にはロジバンにドハマリして人工言語の世界にやってきました。その頃はあまりちゃんとした日本語での学習リソースもなく、一方で英語圏ではようやく初学者向けの分かりよいロジバン講座ができたのもあって、おかゆはその日本語訳から始まり、日本の人工言語界の文化も踏襲して「はじめてのロジバン」を書き下ろしました。第2版を書いている途中で数億年の月日が経ちましたが、関係者のみなさまには多大なるご迷惑をおかけしております。誰か続き書いてくれんかな。
基本的には「ロジバンの人」として佇んでおりましたが、自作の言語もいくつか作ろうとしてて、ログに残ってるものとしては、xaana palaadiとか、縁語やその派生のエニシキ、ロジバンmodとしてのiugbanなどがあると思います。中でも一番有名なのは「アラズ語」ですね。今でもたまにツイッターで言及されているのを見かけるし、なぜか細く長く愛されていますね。ありがたいです。
あと、同時に、分析哲学(言語哲学)も非常に関心があって、「言語ってなんだろう」というところから興味があることが多いです。アラズ語はまさに「人工言語とは何なんだろうな」というような問いから出てきたかもしれません(覚えてません)。
ここたくさん書いても仕方ないか。次行きますね。
長いので消しました。
人工言語って虚無じゃないですか
本題です。
人工言語(実際、言語がそうかもね)は本質的に虚無です。虚無なので、最終的に目標は「いかにして他人にその存在を錯覚させるか」ということになってきます。他人にはいわゆる自分ももちろん含まれますが、殊に自分に対してはピンポイントに統合失調を引き起こせば解決します。
本質的に虚無なので、我々はそれを支持する別存在、世界背景や文化、小説、音声や動画といったコンテンツにやがて執着していくわけです。とはいえ、まずその言語を「あるかも」と思わせる最初の道具は、やっぱり文法書と辞書になると思います。逆に言えば、文法書と辞書だけがその人工言語の所在を知っているわけで、その有り様(書きザマやその形態もちろん含まれます)はその言語の「鏡」です。言い方を変えると、「文法書」や「辞書」は、人工言語においてはそれ自体が既に作品として曝されてるんですよね。
おかゆは度々「人工言語はフィールドワーク的に作ったほうがいい」という風に言っていますが、これは「人工言語は開発する」ものではなく「探索する」ものだという意味あいです。少なくとも第三者への見せ方としては。「開発」という言葉遣いは、もうその時点で既に「その言語は虚無です」と言ってしまっているようなものなので、自ら、その虚構性を認めてしまっています。どうせなら錯覚させませんか?既にあなたの頭には「ある」んですから。
アラズ語は、虚無自体に言語っぽい名前とそれらしい説明をつけただけなんですが、みんな面白おかしく「言語」のひとつとして受け入れてしまってくれていますね。みなさんお気づきでないかもしれませんが、実はアラズ語というのは、無なんですよ!あれのどこが【言語】なんですか?でもやっぱり言語なんですよね。人工言語ってそういうものなんだろうなというのがおかゆの考えです。
人工言語ってマジで無いんですよ。だから「うまい表し方」があるだけです。じゃあその「うまい表し方」ってなんなんでしょうね?それはたぶん付喪神の憑かせ方と同じで、いかに執着して愛着するか、というのが現状の最良の答えです。
とはいえ、冷たい目でみれば、どんなに情熱や執念をもったところで、出来上がるのは「無いものをあるように見せるための一連のテキスト」です。これってハッキングできそうじゃないですか。おかゆが人工言語自動作成に関心があるのは、まさにこの「中国人の部屋」に関してです。本質が虚無だからこそ、インターフェースがすべての意味をなす。そのインターフェースを模倣するようなアルゴリズムが作れたら、もうそれって「執念と情熱を費やした人工言語」なんじゃないかと思うんですけど、どう思います?「表層から内実を覗く」という構図を本質的にもつ人工言語は必ずいつかこの危機に曝されると思います。ドキドキしますね。
工学言語畑にいながら、求める人工言語の姿は結構ファンシーだなと書きながら思いました。工学言語畑にいたからこそかもしれません。ハッキングしてぜんぶ滅ぼしたいと思う一方で、滅ぼせない領域にまで人工言語の追求が及んでいてほしいという気持ちもあります。少なくともくだらんハックに惑わされないように、きちんと人工言語の根っこを掴んでいたいよね。そのためには既存の言語学的なフレームワークから抜け出して、人間というか想定話者というか、そういった対象の意識の傾向を掴まないといけないと思います。
飽きてきたので終わります。ばいばい
ドレミファソラシドの間
めちゃくちゃ久しぶりに書く割にクソどうでもいい話
黒鍵の音、いい読み名ないんか?
ドデレリミファフィソサラチシ
個人的には
- ド# ダ
- レ♭ ル
- レ# リ
- ミ♭ モ
- ファ# フィ
- ソ♭ ス
- ソ# サ
- ラ♭ ロ
- ラ# リャ
- シ♭ ショ
な感じしますよね。